Let's meditate a bit on the following functions:

1. f(x,y) = sqrt(x*y)
2. f(x,y) = 2/(1/x + 1/y)

They are the geometric and the harmonic mean, both of which take a list of numbers, in this case two, and return a "summary" of the two numbers.

Both of these are very similar for practical real world use-cases, so let's focus on the geometric mean for now. What does it look like?

Interesting, so it's only defined (for real numbers) if x and y have the same sign. Makes sense, could have thought of that before. Now let's dig into it's shape in the defined areas.

Also unsurprisingly, we get square root behavior for the individual dimensions. Overall that means we now have a function that is small towards zero, and larger towards larger values of x and y. Now what about it?

The Geometric Mean For Combining Scores

Turns out, the geometric and the harmonic mean are great for combining multiple metrics into one. For example you want to prepare a meal, and have cost and taste, both values in [0,1]. You can get a nice combined score by using the geometric mean of both.

But wait, I hear you say. Why the geometric mean? I can also just use my every day - arithmetic - mean. Well yes, but it will probably not give you what you want. As an extreme example, let's say the meal scores a 1.0 in cost (because it's affordable), but a 0.0 in taste. The arithmetic mean would give you a total score of 0.5. However, you would probably not rank this meal as a 0.5, because it didn't taste well. The geometric mean gives this meal a 0.0.

For many real-world score collections, having one very low value is disqualifying. If your car scores a zero for safety, but a 1.0 for fuel efficiency, you still can't take it. The geometric and harmonic mean act here as a soft "AND" gate. They will only be large if both metrics are large. For binary values, they are exactly AND.

This is also how the harmonic mean is often used in classification: We want a threshold that maximizes recall AND precision at the same time.

Which One To Choose?

Now, which of the two to pick? I think for all practical purposes, it doesn't matter. Both of them have the same overall behavior, and their difference is just a matter of weighting. In the limit, the shape of these functions approaches min(x,y), where only the worst entry determines the result. All of these belong to the Generalized Means.

What About Combining Errors?

What we've seen above is only useful for scores or fitnesses, so values that are bounded by zero and increase with "goodness". How would we make use of this for errors, meaning values that increase with badness? The requirements would be

1. mean error is zero only if both inputs are zero
2. increasing either error increases overall error (OR)

The first idea would be to simply negate the input values. However that doesn't work, since they need to have the same sign. And if both are negative, we have exactly the same metric as before (zero if either is zero).

The next idea would be to take the inverse of the mean, but that also doesn't change the behavior of the function. We need a different function.

So let's turn to the other generalized means. Geometric and Harmonic were the generalized means with p=0 and p=-1 respectively. Approaching min(x,y) with decreasing p. The artihmetic mean is the generalized mean with p=1. If we go in the other direction, we'll have max(x,y) as the limit. And this is precisely what we want. If either x or y is large, max is large. Only if both are small, so is the max.

This looks much better! As it turns out, the Root-Mean-Square (RMS) is also a generalized mean, neat! Unfortunately the "soft AND" doesn't translate to the OR case, because it would need to be perfectly flat to be exactly 1 at (1,0), (0,1) and (1,1), i.e. the max(x,y) function.

If we take a look at the integral curves of the gradients of either function, we can see their behavior (if the means were an optimization target). To maximize the geometric mean (a score), we need to increase both input scores. For the cubic mean (an error), let's follow the gradients backwards, toward smaller numbers of the mean. We see that the mean error only gets smaller if both input errors tend towards zero.

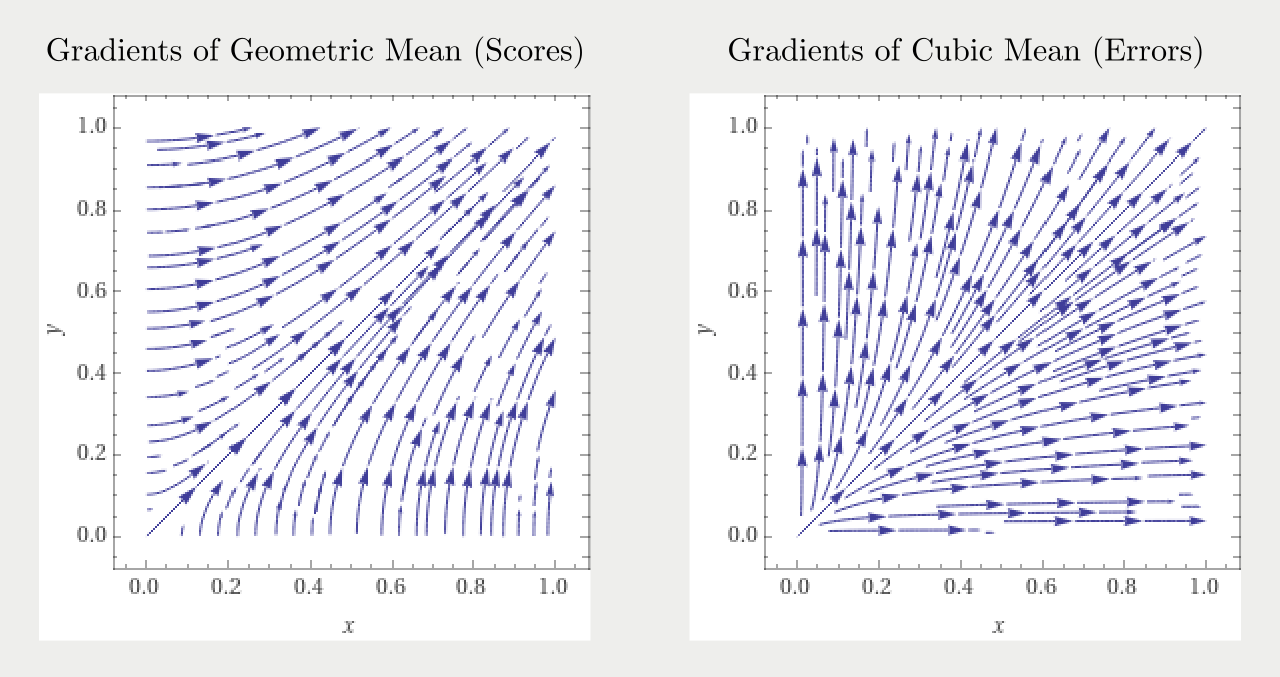
Conclusion

When trying to combine multiple metrics, either positive or negative ones, it pays off to look further than just averaging them using the arithmetic mean. There are other choices with useful consequences, maybe one of the means here is useful to your next project :)